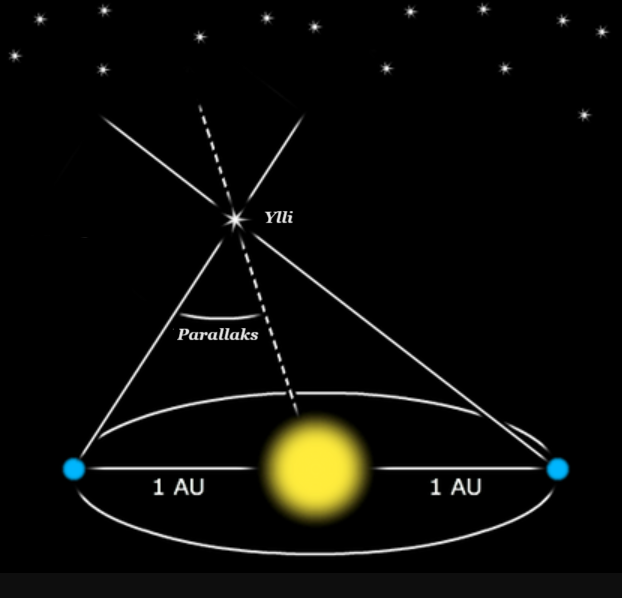
Efekti me të cilin pozicioni ose drejtimi i një objekti duket se ndryshon kur shikohet nga pozicione të ndryshme, quhet parallaks.
P.sh. nëpërmjet shikuesit dhe lentes së një kamere: “ajo që shihni në shikues (monitor) nuk do të jetë krejt ajo që ju merrni në fotografi për shkak të gabimit parallax”
Sasia këndore e parallaksit në një rast të veçantë, veçanërisht ajo e një ylli që shihet nga pika të ndryshme në orbitën e Tokës: “ai arriti të matte parallaksin e yllit 61 Mjellma”
Parallaks quhet këndi nën të cilin prej objektit shihet baza e vrojtimit. Për caktimin e largësive të trupave qiellor shfrytëzohet dukuria e zhvendosjes paralaktike. Zhvendosje paralaktike është lëkundja këndore e lëndës (objektit) e shkaktuar me zhvendosjen e vrojtuesit. Këtë mundësi e shfrytëzojnë shumë adhurues të matjeve në natyrë, astronomët, ushtarët, gjeodet, inspektor, polic si dhe për çfarëdo matje për caktimin e largësisë së trupave të ndryshëm si dhe largësinë e trupave qiellorë.
Shembull:
Sa është largësia e objektit A, prej pikës C në anën tjetër të lumit me ujë ?
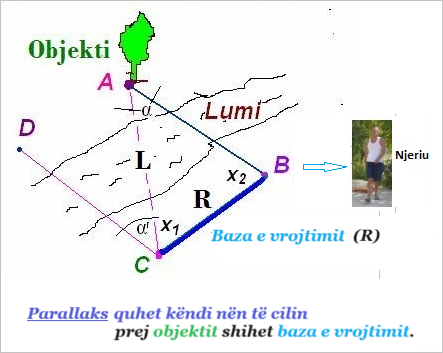
-figura: parallaks
Personi që bënë matjen në pikën B, zgjedhë këtë metodë;
1. Prej pikës B me instrument për matjen e këndeve, këndmatës , caktohet këndi i drejtë ABC, (X2 =900).
2. Për këtë qëllim zgjidhet pika C në bregun ku është personi.
3. Caktohet një bazë, R, me madhësi të njohur BC – baza vrojtuese, e cila matet lehtë, preciz e saktësisht.
4. Prej pikës C matet (caktohet) këndin BCA, (X1 ose α’), Trekëndëshat: CAB=CAD dhe këndet α=α’
Do të gjendet trekëndëshi me dy kënde të shtrira në anën e njohur të gjatësisë me bazë BC.
Parallaks në këtë rast është këndi CAB, këndi alfa α .
Nëse matet dhe shënohet këndi i bazës BC me objektin A (këndi α’), mund të llogaritet largësia e objektit A, pa e matur direkët me mjete, por duke përdor rregullat trigonometrike.
L=R/sinα
Largësia (AB)2 = L2 + R2 caktohet prej teoremës së Pitagorës.
Me këtë rast konstruktivishtë (trigonomikishtë) mund të njehsohet gjatësia e dy anëve BA dhe CA që do të thotë largësinë e objektit A që gjendet në anën tjetër në bregun e lumit.
Zhvendosja parataktike e këndit DCA (drejtimi prej pikës C kah objekti A dhe D), është e barabar me këndin CAB, (drejtim prej pikës A kah pika B dhe C).
Parallaks quajë (quajmë) këndin nën të cilin prej objektit shihet baza e vrojtuar. Në këtë rast Parallaks do të jetë këndi CAB (BAC), fig parallaks.
Në largësinë e dhënë me zgjatjen e bazës vrojtuese zmadhohet edhe saktësia e matjes parallakse, prandaj shtohet edhe saktësia e të caktuarit të asaj largësie.
Parallax
– Wikipedia (1)
Parallaksi është një zhvendosje ose ndryshim në pozicionin e dukshëm të një objekti të shikuar përgjatë dy vijave të ndryshme të shikimit dhe matet me këndin ose gjysmë-këndin e prirjes midis këtyre dy vijave. Për shkak të parashtrimit, objektet e afërta tregojnë një parallaks më të madh se objektet më të largëta, kështu që parallaksi mund të përdoret për të përcaktuar distancat.
Për të matur distanca të mëdha, të tilla si distanca e një planeti ose një ylli nga Toka, astronomët përdorin parimin e parallaksit. Këtu, termi parallax është gjysmë-këndi i prirjes midis dy vijave të shikimit ndaj yllit, siç vërehet kur Toka është në anët e kundërta të Diellit në orbitën e saj. [a] Këto distanca formojnë rungun më të ulët të asaj që quhet “shkalla kozmike e distancës”, e para në një sërë metodash me anë të të cilave astronomët përcaktojnë distancat ndaj objekteve qiellore, duke shërbyer si bazë për matjet e tjera të distancës në astronomi duke formuar shkallët më të larta të shkallëve.
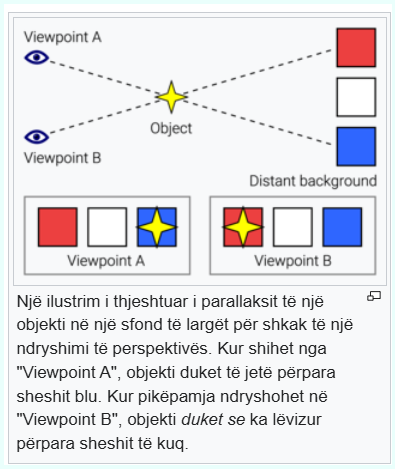
Parallaksi gjithashtu ndikon në instrumentet optike të tilla si fushëveprimet e pushkës, dylbitë, mikroskopët dhe kamerat reflekse me dy lente që shohin objekte nga kënde pak të ndryshme. Shumë kafshë, së bashku me njerëzit, kanë dy sy me fusha vizuale të mbivendosura që përdorin parallaksin për të fituar perceptimin e thellësisë; Ky proces njihet si stereopsis. Në vizionin kompjuterik efekti përdoret për vizionin stereo kompjuterik, dhe ekziston një pajisje e quajtur një rangefinder parallax që e përdor atë për të gjetur gamën, dhe në disa variacione gjithashtu lartësi në një objektiv.
Një shembull i thjeshtë i përditshëm i parallaksit mund të shihet në tabelat e bordeve të automjeteve motorike që përdorin një speedometër mekanik të stilit gjilpërë. Kur shihet nga direkt përpara, shpejtësia mund të tregojë saktësisht 60, por kur shihet nga sedilja e pasagjerit, gjilpëra mund të duket se tregon një shpejtësi pak më ndryshe për shkak të këndit të shikimit të kombinuar me zhvendosjen e gjilpërës nga avioni i cadrës numerike.
–
Parallaksi në astronomi
(2) Parallax | Astronomy, Optics & Measurement | Britannica
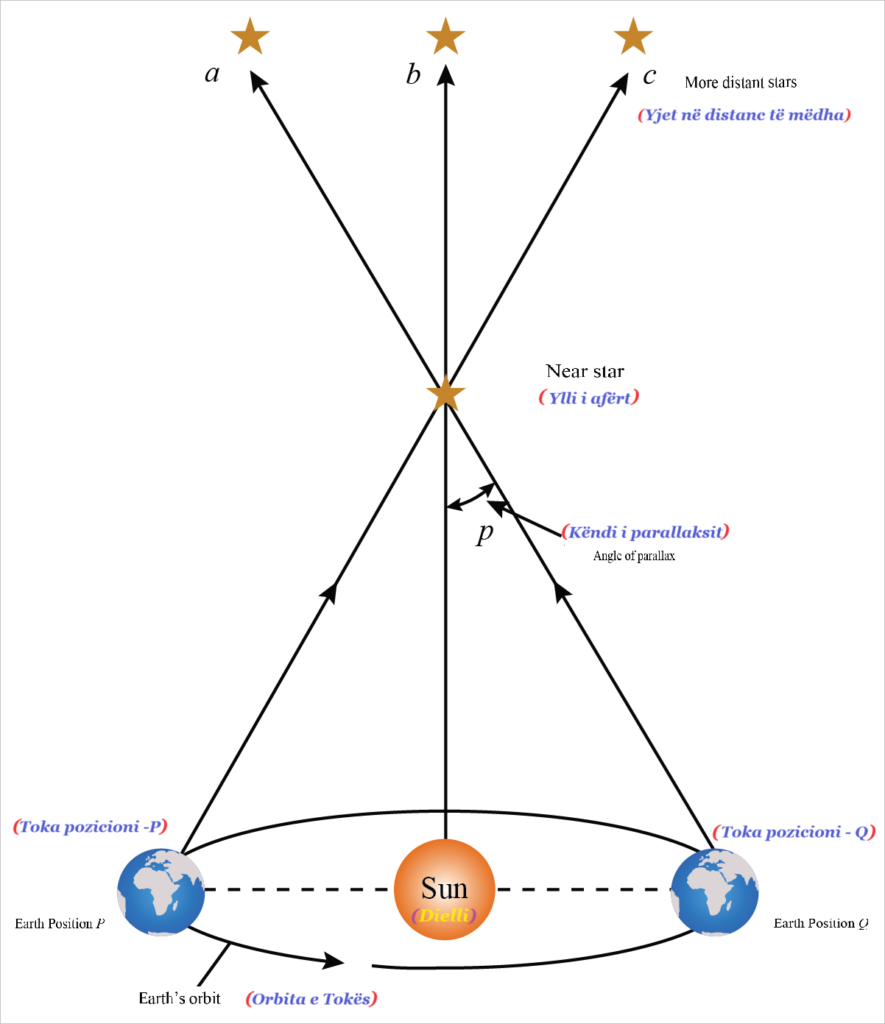
Parallaksi, në astronomi, dallimi në drejtim të një objekti qiellor siç shihet nga një vëzhgues nga dy pika të ndara gjerësisht. Matja e parallaksit përdoret drejtpërdrejt për të gjetur distancën e trupit nga Toka (parallaksi gjeocentrik) dhe nga Dielli (parallaksi heliocentrik). Dy pozicionet e vëzhguesit dhe pozicioni i objektit formojnë një trekëndësh; Nëse vija bazë midis dy pikave vëzhguese është e njohur dhe drejtimi i objektit siç shihet nga secila është matur, këndi apex (parallax) dhe distanca e objektit nga vëzhguesi mund të gjenden thjesht.
Në përcaktimin e një distance qiellore me matjen e parallaksit, vija bazë merret sa më gjatë që të jetë e mundur në mënyrë që të përftohet saktësia më e madhe e matjes. Për Diellin dhe Hënën, vija bazë e përdorur është distanca midis dy pikave të ndara gjerësisht në Tokë; Për të gjithë trupat jashtë sistemit diellor, vija bazë është boshti i orbitës së Tokës. Parallaksi yjor më i madh i matur është 0,75″, për yllin më të afërt, Alpha Centauri; Më e vogla që mund të matet drejtpërdrejt është rreth 25 herë më e vogël, por metodat indirekte të diskutuara më poshtë llogaritjen e lejes së parallaksit, inversement proporcionale me distancën, për objekte gjithnjë e më të largëta por edhe me gjithnjë e më shumë pasiguri.
–
etj
–
Reference