Ligjet e Keplerit për Lëvizjen e Planetëve

Ligjet e Keplerit për lëvizjen e planetëve janë nxjerrë nga astronomi gjerman Johannes Kepler, analiza e të cilit me vëzhgimet e astronomit danez të shekullit të 16-Tycho Brahe ia ka mundësuar për të njoftuar dhe publikuar dy ligjet e tij të parë në vitin 1609 dhe një ligj të tretë pothuajse një dekadë më vonë, në vitin 1618.

Johannes Kepler, duke punuar me të dhënat e mbledhura me kujdes nga Tycho Brahe pa ndihmën e një teleskopi, zhvilloi tre ligje që përshkruanin lëvizjen e planetëve nëpër qiell.

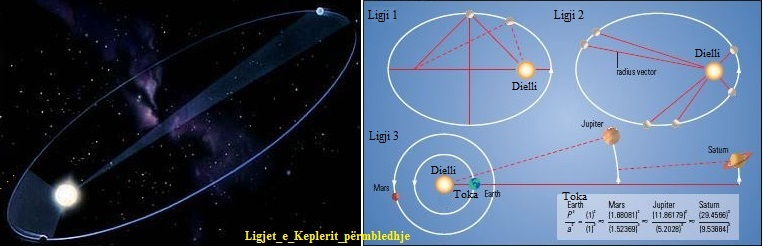
1. Ligji i Orbitave: Të gjithë planetët lëvizin në orbita eliptike, me diellin në një fokus.

2. Ligji i Zonave: Një linjë që lidh një planet me diellin fshin zonat e barabarta në kohë të barabarta.

3. Ligji i Periudhave: Katrori i periudhës së çdo planeti është proporcional me kubin e boshtit gjysmë i madh të orbitës së tij.

Ligjet e Keplerit rrjedhin për orbitat rreth diellit, por ato zbatohen edhe për orbitat satelitore. – (¹) (Kepler’s Laws (gsu.edu)

Johannes Kepler (1571- 1630) ka botuar tre ligjet e lëvizjes planetare, dy të parët në vitin 1609 dhe e treta në 1618. Ligjet janë bërë të mundur nga të dhënat planetare me saktësi të paparë të mbledhura nga Tycho Brahe. Ligjet ishin të dy një largim radikal nga paragjykimet astronomike të kohës së vetë dhe mjeteve të thella për parashikimin e lëvizjes planetare me saktësi të madhe. Kepler, megjithatë, nuk ishte në gjendje të përshkruajë në mënyrë të konsiderueshme pse ligjet funksiononin në atë mënyrë.

Në shkencën e deriatëhershme nuk është paraqitur një bashkëpunim më frytëdhënës sikurse u krijua nga çifti Brahe — Kepler, sepse njëri kishte atë çka tjetri nuk e kishte, kurse të dytë përbënin një tërësi.

Johan Kepleri (1571- 1630) i bashkëngjitet Brahes në pallatin Benatek, në periferi të Prages, në shkurt të vitit 1600. Meqë asistenti i Brahes, Longomontani, kishte problem me Marsin, vrojtimet e tij i vazhdoi Kepleri ambicioz. Është fat që u zgjodh pikërisht Marsi, sepse është planeti më i përshtatshëm për zbulimin e elipticitetit. Si rezultat i punës 20 vjeçare, Kepleri arriti në zbulimin e tri ligjeve të lëvizjes së planetëve, të cilët janë bazë e astronomisë moderne.

/-

Në astronomi, ligjet e Keplerit për lëvizjen planetare, të botuara nga Johannes Kepler midis viteve 1609 dhe 1619, përshkruajnë orbitat e planetëve rreth Diellit. Ligjet ndryshuan teorinë heliocentrike të Nicolaus Copernicus, duke zëvendësuar orbitat rrethore dhe epiciklet e tij me trajektore eliptike dhe duke shpjeguar se si ndryshojnë shpejtësitë planetare.

Tre ligjet thonë se:

1. Orbita e një planeti është një ellipse me Diellin në një nga dy foci (fokuse).

2. Një segment i linjës që bashkohet me një planet dhe Dielli fshin zona (sektor) të barabarta gjatë intervaleve të barabarta kohore.

3. Katrori i periudhës orbitale të një planeti është proporcional me kubin e gjatësisë së boshtit gjysmë të madh të orbitës së tij.

Orbitat eliptike të planetëve u treguan nga llogaritjet e orbitës së Marsit. Nga kjo, Kepleri nxori në pah se trupa të tjerë në Sistemin Diellor, duke përfshirë edhe ata më larg Diellit, kanë edhe orbita eliptike. Ligji i dytë ndihmon për të përcaktuar se kur një planet është më afër Diellit, ai udhëton më shpejt. Ligji i tretë shpreh se sa më larg të jetë një planet nga Dielli, aq më e ngadaltë është shpejtësia e tij orbitale dhe anasjelltas.

Isak Njutoni tregoi në vitin 1687 se marrëdhëniet si Kepleri do të aplikoheshin në Sistemin Diellor si pasojë e ligjeve të tij të lëvizjes dhe ligjit të gravitacionit universal.

Një qasje më e saktë historike gjendet në Astronomia nova dhe Epitome Astronomiae Copernicanae.

• Imazhi nga Wikipedia> – (²) (Kepler’s laws of planetary motion – Wikipedia) –

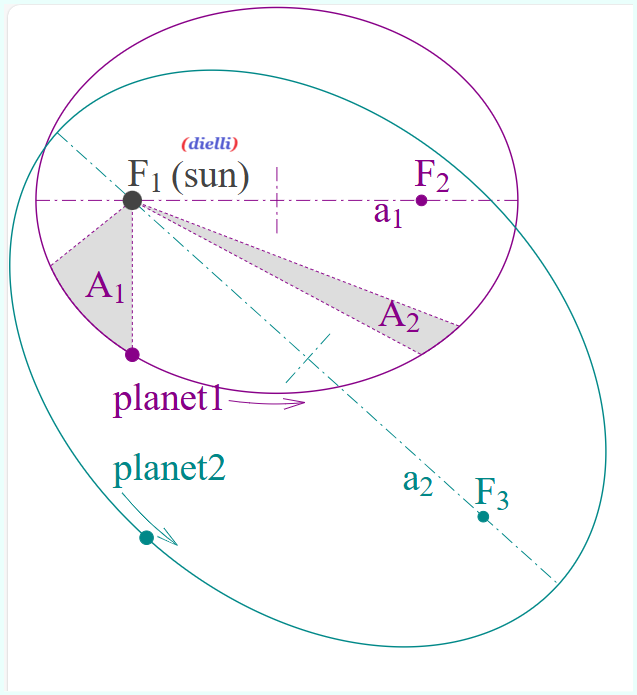
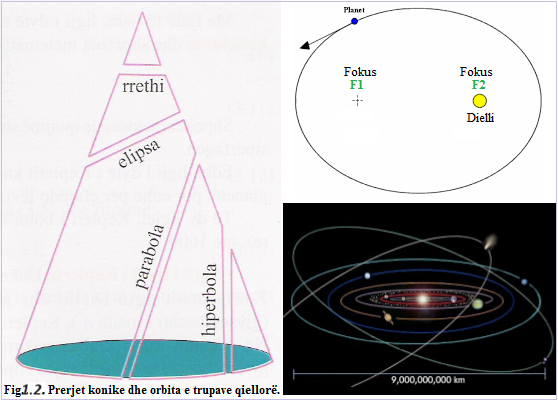
– Ilustrim i ligjeve të Keplerit me dy orbita planetare. Orbitat janë ellipse, me foci (fokus) F1 dhe F2 për Planetin 1, dhe F1 dhe F3 për Planetin 2. Dielli është në F1. Zonat me hije A1 dhe A2 janë të barabarta, dhe janë fshirë në kohë të barabarta nga orbita e Planetit 1. Raporti i kohës së orbitës së Planetit 1  është me atë të Planetit 2.

Diagrami që ilustron ligjet e Keplerit: 1. Dy orbita eliptike me gjysmë akse të mëdha a₁ dhe a₂ dhe pika fokale qendrore F₁, F₂ për planetin 1 dhe F₁, F₃ për planetin 2. Dielli në F₁. 2. Dy sektorët A₁, A₂ të sipërfaqes së barabartë janë përfshirë në kohë të barabartë. 3. Raporti i periudhave orbitale t₂/t₁ është (a₂/a₁)^3/2.

Ligji i parë i Keplerit

Duke pasur në disponim numër të madh vrojtimesh të trashäguara nga Tiho Brahe, Kepleri provoi shumë orbita të formave të ndryshme, p.sh., rrathë, ovale, por nuk gjeti përputhshmëri me vrojtimet që kishte në dispozicion. Më në fund, kur për orbitë propozoi elipsën, në njërën vatër të së cilës vendosi Diellin, fitoi pajtueshmëri me vrojtime. Pra, sipas Keplerit, u bë kalimi nga orbitat rrethore të Kopernikut në orbita eliptike. Kjo është pärmbajtje e ligjit të parë të tij, i cili thotë: Planetët lëvizin rreth Diellit nëpër orbita eliptike, në njërën vatër të së cilëve ndodhet Dielli. Natyrisht se ky ligj ka përmbajtje më të gjerë dhe nuk vlen vetëm për planetë, por për të gjithë trupat që lëvizin nën veprimin e forcës tërheqëse.

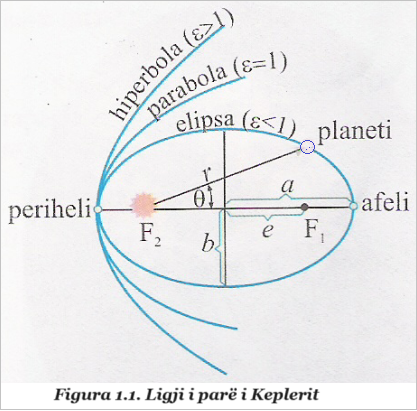
Si e cekur, afel (A) quajmë pikën më të largët të pozitës së planetit rreth Diellit, ndërsa perihel (P) — pikën më të afërtë, siç tregon fig. 1.1. Fig. 1.1. Ligji i parë i Keplerit.

–

Nëse boshtin e sistemit të koordinatave polare me qendër në Diell e orientojmë kah afeli, do të fitojmë ekuacionin e ndërrimit të largësisë mes Diellit dhe planetit (ndërrimin e rreze vektorit):

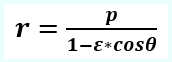
ose r=p/1-ε*cosθ …. formula (1.a)

Këtu p — paraqet parametrin e elipsës, i cili për planetë ka vlerën:

p=4C²/GM …. formula (1.b)

ku G=6.672*10¹¹ (Nm²/kg²)

ku C-është shpejtësia sektoriale e planetit (shiko ligjin e dytë të Keplerit), G– konstanta univerzale e tërheqjes, M– Masa e Diellit, kurse θ – këndi polar që mbyll rreze vektori që bashkon pozitën e Diellit dhe planetit me boshtin që kalon nëpër Diell dhe afel, siç tregohet në fig. 1.1.

Madhäsia ε, nga vlera e së cilës varet edhe rruga e planetit, quhet ekscentricitet numerik dhe është e barabartë me:

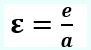
ε=e/a …. formula (1.c)

ku: e — është largësia nga qendra e elipsës deri në fokus ose vatër (ekscentriciteti linear), ndërsa a — gjysmëboshti i madh i elipsës. Prerjet konike i kanë nga dy ekscentricitete, linear dhe numerik.

Ekuacioni (1.a), që ndryshe quhet ekuacion i prerjeve konike (fig. 1.2.), në koordinata polare tregon se ligji i parë i Keplerit ka kuptim më të gjërë, sepse nuk parasheh vetëm lëvizje të mundshme të trupit qiellor nëpër rrugë të mbyllura, siç është elipsa, por edhe nëpër rrugë parabolike ose hiperbolike. Rrethi, elipsa, parabola dhe hiperbola fitohen si prerje e një rrafshi në pozita të ndryshme me konin, siç tregohet në fig. 1.2, kurse ekuacioni i tyre fitohet nga (1.a) për vlera të ndryshme të ε. Pra, për ε=0 fitojmë rrethin, për ε<1 rruga është elipsë, për ε=1 rruga është parabolë dhe për ε>1 rruga është hiperbolë.

Forma e rrugës varet prej energjisë së përgjithshme E të trupit qiellor, përkatësisht prej shpejtësisë fillestare (te satelitët artificialë).

Planetët lëvizin rreth Dielit nëpër orbita eliptike, sepse elipsa nuk ka pika pambarim të larguara, por ekzistojnë edhe trupa të tjerë qiellorë, e veçanërisht që njëherë kometat hyjnë në fushë tërheqëse të Diellit dhe nuk paraqiten më kurrë pranë tij. Rrugët e kometeve mund të jenë parabolike dhe hiperbolike.

Ligji i parë i Keplerit ka kuptim më të gjerë, sepse nuk vlen vetëm për lëvizje të planetëve, por edhe për lëvizje të satelitëve rreth planetëve ose për lëvizje të satelitëve artificialë rreth Tokës. Figura 1.2. Prerjet konike dhe orbita e trupave qiellorë.

–

Ligji i dytë i Keplerit

Duke tentuar të shpjegojë ndryshimin e lëvizjes së planetit rreth Diellit, Kepleri diktoi vlerën konstante të prodhimit të katrorit të rreze-vektorit që bashkon pozitën e planetit me Diellin me këndin qëndror të vrojtuar në intervale kohe të barabarta, siç shihet nga tabela IV.

TABELA IV

Dita	r2	r2 Δθ
2.I	0.9669	3548
2.II	0.9720	3547
2.III	0.9821	3547
2.IV	0.9490	3547
2.V	1.0157	3547
2.VI	1.0287	3547
2.VII	1.0377	3547
2.VIII	1.0300	3547
2.IX	1.0181	3547
2.X	1.0018	3547
2.XI	0.9847	3547
2.XII	0.9720	3547

Në këtë mënyrë ai arriti deri te ligji i sipërfaqeve të barabarta që thotë: Rreze vektori që bashkon pozitën e Diellit me planetin në kohë të barabarta përshkruan sipërfaqe të barabarta. Kjo tregon se planeti në afel lëviz më shpejt sesa në perihel, sepse sektorët e hijesuar në fig. 2.1, e kanë të njëjtën sipërfaqe. Fig. 2.1. Ligji i dytë i Keplerit.

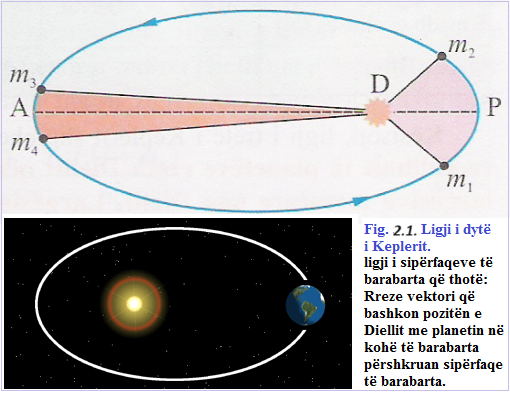
Me fjalë të tjera, ligji i dytë thotë se shpejtësia sektoriale e planetit është konstante dhe shprehet matematikisht në formën:

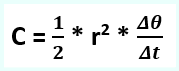
….. formula (2.a) – Shpejtësi sektoriale (zonale).

Shpejtësi sektoriale (zonale) quajmë shpejtësinë me të cilën rreze vektori e përshkruan sipërfaqen.

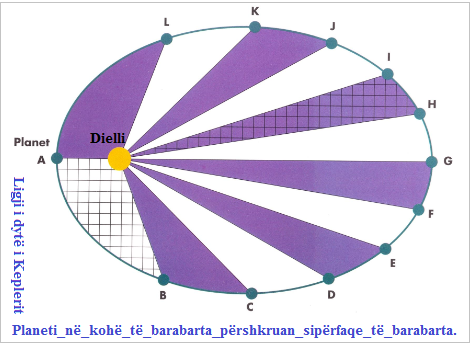
-Imazh 2a: Planeti në kohë të barabarta përshkruan sipërfaqe të barabarta.

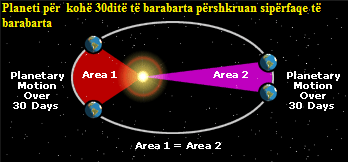
-Imazh 2b: Planeti në kohë 30 ditë të barabarta përshkruan sipërfaqe të barabarta.

Edhe ligji i dytë i Keplerit ka kuptim më të gjerë, sepse nuk vlen vetëm për planetë, por edhe për çfarëdo lëvizje rreth qendrës terheqëse.

Të dy ligjet, Kepleri i botoi në veprën “Astronomia nova” (Astronomia e re), me 1609.

–

Ligji i tretë i Keplerit

Duke kërkuar lidhshmëri mes periodës së rrotullimit T të planetit rreth Diellit dhe përmasave të elipsës nëpër të cilën ai lëviz (gjysmëboshti i madh a), Kepleri provoi shumë raporte mes këtyre madhësive. Në veçanti, kur i krahason katrorët e periodave të rrotullimit me kubet e gjysmëboshteve të mëdhenj të elipsave përkatës të planetëve fitoi vlerë konstante, siç shihet në tabelën vijuese V.

TABELA V

	Merkuri	Venera	Toka	Marsi	Jupiteri	Saturni
Katrori i periodës (T2)	0.058	0.378	1	3.54	140.7	867.7
Kubi i gjysmëboshtit të madh të elipsës (a3 )	0.058	0.378	1	3.54	140.8	867.9
Raporti T2/a3	1	1	1	1	1	1

Kësisoji, ligji i tretë i Keplerit shprehet në formën: Katrorët e kohëve të rrotullimit të planetëve rreth Diellit qëndrojnë proporcional me kubet e largësive mesatare nga Dielli. Largësia mesatare është e barabartë me gjysmëboshtin e madh të elipsës, sepse Dielli gjendet në fokus (vatër) të saj.

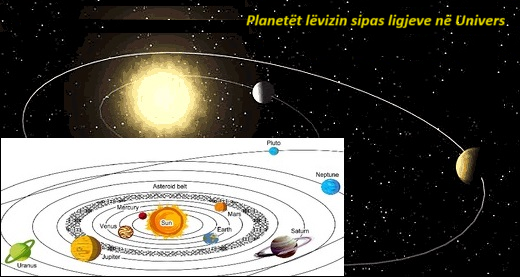
-Imazh: Planetët lëvizin sipas ligjeve në Univers.

Matematikisht, këtë ligj mund ta përfitojmë në këtë mënyrë. Meqë elipsa është lakore e mbyllur, mund ta përkufizojmë kohën e një rrotullimi të plotë nëpër të që do ta shënojmë me T. Meqenëse C është shpejtësia sektoriale (zonale), atëherë prodhimi C*T paraqet sipërfaqen që përshkruan vektori i pozitës gjatë një rrotullimi e kjo është sipërfaqja e elipsës. Pra:

C*T=a*b*π     … (3.8)

Këtu me a kemi shënuar gjysmëboshtin e madh, ndërsa me b gjysmëboshtin e vogël të elipsës. Nga gjeometria e dimë se parametri p i elipsës me gjysmëboshte ka këtë lidhshmëri:

 p=b²/a … (3.9)

E ngrisim (3.8) në katrorë:

C² * T² =a² * b² * π² … (3.10)

nga (3.9) rrjedh se:

b² = p*a    … (3.11)

E zëvendësojmë (3.11) në (3.10):

C² * T² =a³ * p * π²    … (3.12)

E zëvendësojmë vlerën e parametrit p në formulën (1.b); p=4C²/GM

dhe fitojmë:

… formula (3.13) konstanta K.

Zakonisht, ky ligj zbatohet për dy pozita (1) dhe (2) e të njëjtit trup apo për dy trupa të ndryshëm qiellorë në formën:

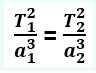
ose e shtruar; T₁²/a₁³ = T₂²/a₂³ …. formula (3.14)

Shprehja (3.14) shërben për zgjidhje të shumë problemave në astronomi.

–

Heto edhe :

Si e zgjeroi Njutoni nocionin e tij të gravitetit për të shpjeguar lëvizjen planetare? (³)

Referenca

1. Kepler’s Laws (gsu.edu) ↩︎
2. Kepler’s laws of planetary motion – Wikipedia ↩︎
3. Kepler’s Three Laws (physicsclassroom.com) ↩︎